If a function or problem is recursive in nature, it means that it is solved only by relying on smaller parts of itself. A good example is the Fibonacci post written on this blog, as the Fibonacci sequence is defined recursively. It relies on the two previous terms of the sequence to add any other numbers. It's important to have a stop condition, or terminating case, otherwise, as you can guess, a recursive function can continue infinitely. In the Fibonacci example, we decremented our argument until we hit 0, then stopped.
Recursive functions implement the calling of their own method in order to compute an answer. Through the use of stacks, answers are chained together, and they rely on other answers to compute the desired one. Before moving on, it's important to define iteration, or iterative development. Loops are a huge component in this, because iteration really means to repeat one set of instructions multiple times. Imagine all the kinds of loops that exist... each pass through the loop is one iteration. When you do it multiple times, you have gone through multiple iterations of the same set of instructions — each leading you closer to the desired answer. Iteration is actually mostly identified with for loops (also known as fancy-man while loops), and has a fixed number of variables that it keeps track of. Iterative methods are arguably easier to trace through, as most changes to each variable are explicit, and not "hidden" by the computer. Though the two, recursion and iteration, are not mutually exclusive, as either can be equally expressed through programs.
Iteration can easily be converted into Tail Recursion, an algorithm which relies on the completion of ALL previous calls to the function before calculating the final answer. A simple implementation of tail recursion can be found in the following cumulative sum program.
1 2 3 4 | //cumulative sum private static int cumSum(int x) { return (x == 1) ? 1 : x + cumSum(x - 1); } |
This method accepts an integer as a parameter, and then makes a decision on what to return. It first checks if that integer that was passed in is 1, and if it is, then it returns 1. If that parameter is not equal to 1, then it takes the parameter and adds it to the result of our same method with our parameter decremented by one. For instance, if we made the call to this function like this: cumSum(3), the program would have to rely on the previous calls to the function, cumSum(2) and cumSum(1). Below is what the method will actually do when we pass in the integer 3.
1 2 3 4 5 6 | cumSum(3) 3 + (cumSum(2)) 3 + (2 + cumSum(1)) 3 + (2 + 1) 3 + 3 6 |
As you can see, it relies on the result of other calls to the function before it computes the final result. The first, bottom "stack" would be the result of cumSum(3), and the stack above that would include the call to cumSum(2), and the stack above that would include the result of cumSum(1), which would then report back to the second stack, and back to the first stack to produce the sum. Because each stack's "tail" is the next call to the function, this is called tail recursion. This can easily be represented by a for loop that walks through every integer less than the parameter and adds it to a running sum. This close relationship in algorithm is why iteration is very much similar to tail recursion. Nowadays, defining the number of and size of your stacks is done already by your high-level programming language, like Java, whereas in the past, the programmer would define the properties of these stacks.
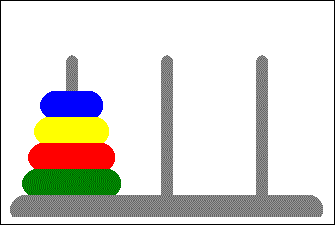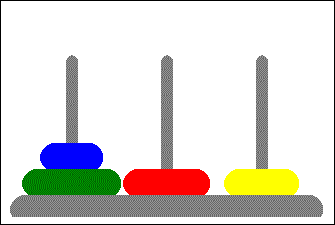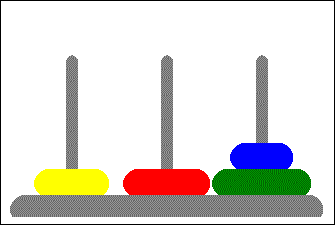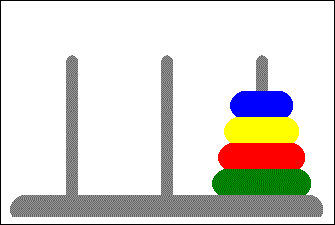
Towers of Hanoi
Recursive algorithms may be more elegant and shorter in length, but not always the most practical or easy to think of.
Another example of a recursive implementation is with the computation of a factorial. Shameless plug to the other part of my blog, where you can read all about it. Seriously, go read about factorials. The two algorithms we will investigate are the iterative implementation, using a loop, and the recursive implementation. In the iterative example, I used a while loop, to gather as many h8rs as possible.
1 2 3 4 5 6 7 8 9 | //iterative factorial private static int factorial(int n) { int walk = n, result = 1; while (walk != 0) { result *= walk; walk -= 1; } return result; } |
Here, we see that we start with two integer variables, walk and result. We start at the parameter, then "walk" through every integer less than our parameter, until we hit 0, then multiply those integers together. This is exactly what a factorial is. Our loop will continue for as long as our "walking" integer is not zero. To ensure we do not infinitely loop, we decrement our "walking" variable by 1 to get the next integer. In the end, we return the factorial of the parameter. Next, we will see the recursive implementation.
1 2 3 4 | //recursive factorial private static int factorial(int n) { return (n == 0 || n == 1) ? 1 : n * factorial(n - 1); } |
At first, you can realize that this is only one freaking line, how is it possible that it even works?? Well, if you want to be technical, there would be an issue if these two methods were in the same class, because they're named the same thing. But let's pretend they're not. The recursive method also takes in an integer as a parameter. Then, it makes a decision on what to return, using an IF-THEN-ELSE statement. It first checks to see if the integer parameter is 0 or 1, and if it is, then it returns 1. If it's neither of those, it will return the product of that integer and the result of factorial with the parameter decremented by 1. If we wanted to find the factorial(3) recursively, the method would call itself to find factorial(2) and factorial(1) before any calculations are made. Though a pitfall of this program is that it fails to handle negative input, it still is effective in that it demonstrates, at a basic level, the power of recursion. There are functions that are recursive that can also be expressed iteratively. There are also functions that can only be expressed recursively. There are also functions, believe it or not, whose definitions are recursive, but fail to provide output for some inputs, which make them extremely difficult to code.
1 2 3 4 5 | /* This post is not complete! Soon to come: defining and explaining the recursive nature of Ackermann-Péter function, as well as how quickly these recursive methods can grow... */ |
Resources
https://www.youtube.com/watch?v=Mv9NEXX1VHc
https://www.youtube.com/watch?v=7t_pTlH9HwA
http://stackoverflow.com/questions/1114047/what-is-the-role-of-stack-in-a-microprocessor